Im letzten Schuljahr haben wir uns schon einmal mit der Binären Suche beschäftigt. Damals haben wir die binäre Suche iterativ implementiert. Nun haben wir uns im Rahmen das Themenkomplexes Rekursion und Backtracking mit der rekursiven Variante des Algorithmuses befasst.
Prinzip:
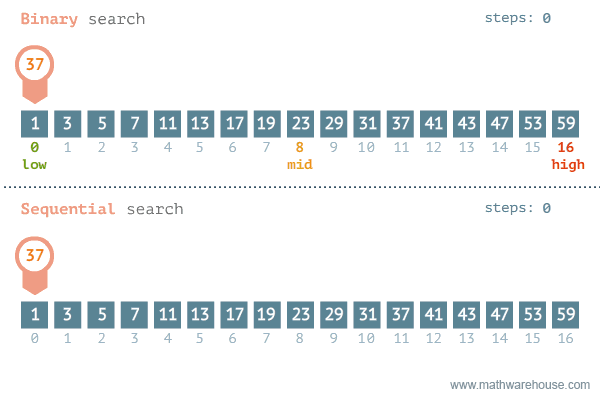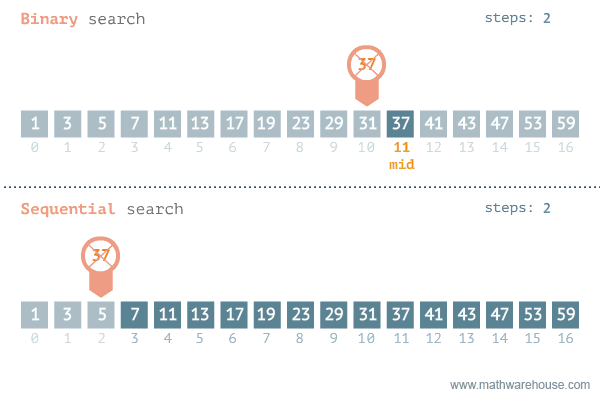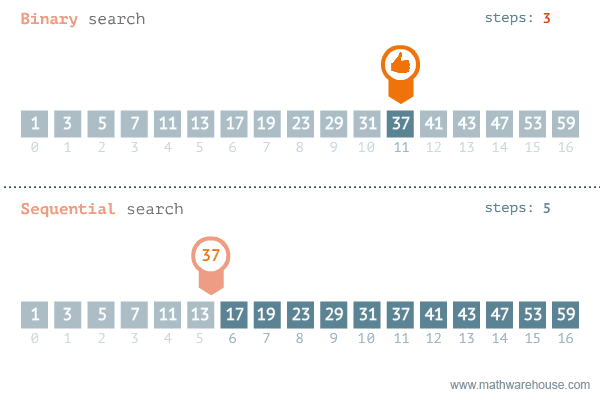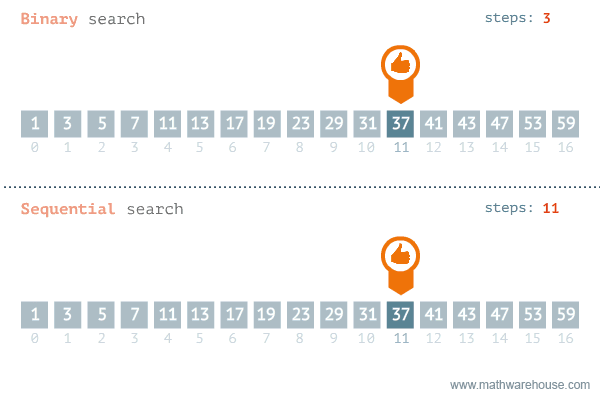Quelle: https://blog.penjee.com/binary-vs-linear-search-animated-gifs/
Wie oben zu sehen ist, wird in der Binären Suche immer der mittlere Wert aus einem sortierten Bereich bestimmt und dann überprüft, ob der gesuchte Wert kleiner oder größer als der mittlere Wert ist. Oder einfacher formuliert: Es wird überprüft, ob der Wert sich links oder rechts von der Mitte befindet.
Pseudo Code
function binSuche(links, rechts, wert)
wenn links = rechts
dann wenn linker wert = wert
gib links zurueck
sonst gib -1 zurueck
sonst wenn mittlerer Wert = wert
gib mittleren Wert zurueck
sonst
wenn mittlerer Wert > wert
dann gib binSuche(links, mitte, wert) zurueck
wenn mittlerer Wert < wert
dann gib binSuche(mitte, rechts, wert) zurueck
Die Methode bekommt als Parameter den Pointer links und rechts übergeben. Sie markieren den zu untersuchenden Wertebereich. Natürlich muss auch der gesuchte Wert mit übergeben werden ( wert).
Sollte nun der linke Pointer gleich dem rechten sein, so ist nur noch ein Wert übrig, der überprüft werden kann. Entweder dieser ist dann der gesuchte Wert, oder nicht. Weiterhin muss überprüft werden, ob der mittlere Wert der gesuchte Wert ist. In allen anderen Fällen kann man davon ausgehen, dass man weitersuchen muss. Dennoch kann man den Wertebereich auf links oder rechts der Mitte eingrenzen .
Implementierung:
public int binSucheRek(int key, int left, int right){
if(left >= right ){
//Beginn Rekursionsbasis:
if(pruefeWert(key,left)) return left; //letzter Wert ist der gesuchte Wert
else return -1; //kein Wert mehr uebrig.
} else if(pruefeWert(key,(left+right)/2)){
return (left+right)/2; //der mittlere Wert ist der gesuchte Wert
}else {
//Beginn Rekursionsschritt
if (array[(left + right) / 2 ] >= key) return binSucheRek(key, left, (left + right) / 2 - 1); //Linker Teil
if (array[(left + right) / 2 ] <= key) return binSucheRek(key, (left + right) / 2 + 1, right); //Rechter Teil
else return -1; //Sonst gib -1 als Fehler zurueck
}
}Struktogramm:
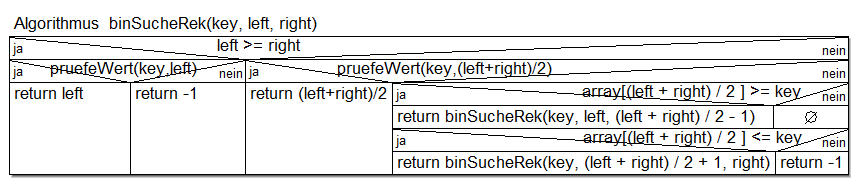
Man kann jede beliebige Klasse ähnlich wie bei dem UML Diagramm auch in einem Struktogramm darstellen. Insbesondere Verzweigungen lassen sich hiermit gut darstellen.
Laufzeiten:
Wie wir in der obigen Animation schon gesehen haben, kann man natürlich auch die Suche linear durchführen. Dabei würde man einfach von Wert zu Wert gehen, und jeden Wert dann mit dem gesuchten Wert vergleichen. Die Geschwindigkeit scheint sich anfangs nicht groß von der der Binären Suche zu unterscheiden. Man nehme aber nun folgendes Beispiel:
Ich haben einen neuen Freund auf einer Party getroffen, und seinen Namen erfahren. Nun möchte ich ihn anrufen, weil er mir mein Geld gestohlen hat. Dafür suche ich dann in einem Telefonbuch ( das ist eine dickes Buch mit Namen und den dazugehörigen Telefonnummern drinnen) den Namen meines Freundes heraus.
Würde ich jetzt linear von A bis Z durch das ganze Buch durchgehen, so würde ich noch sehr lange suchen müssen, bis ich die Nummer gefunden hätte. Wende ich aber die Binäre Suche an, so werde ich meinen Freund relativ schnelle finden. Das heißt, wir stellen fest, dass die Effizienz eines Algorithmus oft von der Anzahl der Werte abhängt.
Eine Tabelle mit Laufzeiten für verschiedene Algorithmen - Quelle
https://www.hackerearth.com/practice/notes/sorting-and-searching-algorithms-time-complexities-cheat-sheet/
Wir unterscheiden dabei zwischen worst, average, und best Case. Besonders aussagekräftig ist dabei der average Case. Bei der Binären Suche ist dieser logarithmisch. Das bedeutet, dass bei einer Erhöhung der Anzahl der Werte von 10 auf 20 die Anzahl der Schritte sich um ca. 1 erhöht. Bei Der linearen Suche verdoppelt sie sich in etwa. Zwar erscheint dabei natürlich die Binäre Suche als die beste Wahl, man muss aber in einer endgültigen Beurteilung berücksichtigen, dass die Menge, die durchsucht wird, auch sortiert sein muss. Das führt je nach Sortieralgorithmus zu längeren Laufzeiten.